My Machine Learning Foundations curriculum provides a comprehensive overview of all of the subjects — across mathematics, statistics, and computer science — that underlie contemporary machine learning approaches. You can check out the full curriculum and all of the open-source Python code (featuring the NumPy, TensorFlow, and PyTorch libraries) in GitHub here.
At a high level, my ML Foundations content can be broken into four subject areas: linear algebra, calculus, probability/stats, and computer science. The first quarter of the content, on linear algebra, stands alone as its own discrete course and is now available on YouTube.
The playlist for my complete Linear Algebra for Machine Learning course is on YouTube here. There are a total of 48 videos partitioned into five thematic segments, as detailed below. Each video in the list has its duration shown alongside it in parentheses.
Segment 1: Data Structures for Algebra
The first segment introduces tensors, the fundamental data structure of linear algebra.
What Linear Algebra Is (24:04)
Linear Algebra Exercise (2:05)
Tensors (2:34)
Scalars (13:05)
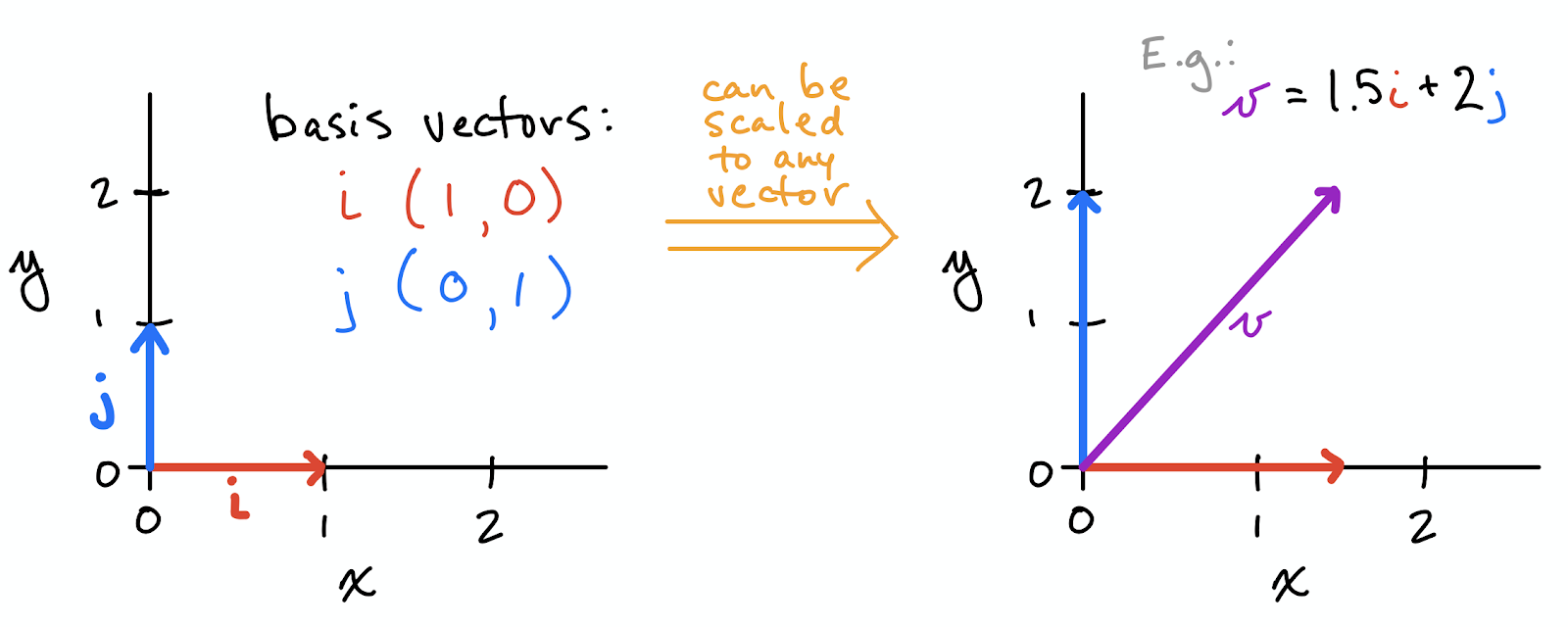
Vectors and Vector Transposition (12:19)
Norms and Unit Vectors (15:10)
Matrix Tensors (8:24)
Generic Tensor Notation (6:44)
Total runtime for Segment 1 is an hour and 41 minutes.
Segment 2: Tensor Operations
This segment covers the critical operations we can perform on tensors.
Segment Intro (1:20)
Tensor Transposition (3:53)
Tensor Reduction (3:32)
The Dot Product (5:14)
Visualizing Linear Systems (11:00)
Total runtime for the second segment is 42 minutes.
Segment 3: Matrix Properties
This segment details the most important properties and classes of matrix tensors.
Segment Intro (2:06)
The Frobenius Norm (5:02)
Matrix Multiplication (25:00)
Matrix Inversion (17:07)
Diagonal Matrices (3:26)
Orthogonal Matrices (5:50)
Orthogonal Matrix Exercises (2:11)
Total runtime for Segment 3 is an hour and six minutes.
Segment 4: Eigenvectors and Eigenvalues
This segment introduces eigenvectors and eigenvalues, special tensors that are associated with any given matrix and that enable countless ML applications.
Segment Intro (17:53)
Applying Matrices (7:31)
Affine Transformations (18:53)
Eigenvectors and Eigenvalues (26:47)
Matrix Determinants (8:05)
Determinant Exercises (1:28)
Determinants and Eigenvalues (16:17)
Eigendecomposition (12:49)
Total runtime for Segment 4 is two hours and 11 minutes.
Segment 5: Matrix Operations for Machine Learning
This segment ties all of the preceding segments together, enabling us to use linear algebra alone to perform powerful ML techniques such as data compression, regression, and clustering.
Segment Intro (3:22)
Singular Value Decomposition (10:50)
Data Compression with SVD (11:33)
The Moore-Penrose Pseudoinverse (12:23)
The Trace Operator (4:37)
Principal Component Analysis (8:27)
Linear Algebra Resources (6:11)
Total runtime for Segment 5 is an hour and 16 minutes.
Total runtime for all five segments — that is, the entire Linear Algebra for Machine Learning course — is 7 hours and 9 minutes. I hope you enjoy every minute of it!